Необходимый напор насоса в неразветвленном трубопроводе получается из уравнения БЕРНОУЛЛИ для одномерных стационарных потоков несжимаемой среды:
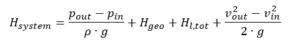
p
in, p
out= давления при всасывании или выпуске уровня жидкости ρ = плотность жидкости g = ускорение свободного падения (9,81 м / с²) H
geo= статическая разница высот между уровнем жидкости в емкостях на стороне всасывания и на стороне нагнетания. H
l, tot= общие потери на трение трубы между входом и выходом v
in, v
out= средние скорости потока во всасывающем и напорном контейнерах Согласно закону непрерывности, средние скорости потока во всасывающем и напорном резервуарах в большинстве случаев незначительно малы и ими можно пренебречь, если поверхности резервуаров относительно велики по сравнению с поверхностями трубопроводов. В этом случае приведенная выше формула упрощается до:
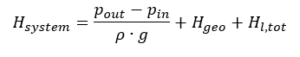
Статическая часть характеристики системы, т.е. та часть, которая не зависит от скорости потока и, следовательно, расхода, равна:
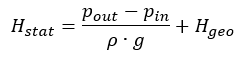
Для закрытых систем это значение равно нулю. Общая сумма потерь складывается из потерь всех компонентов всасывающего и напорного трубопроводов. При достаточно больших числах Рейнольдса он пропорционален квадрату объемного расхода.
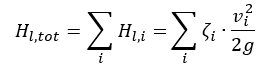
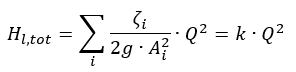
g = ускорение свободного падения (9,81 м / с²) H
l, tot= общие потери на трение между входом и выходом v
i= средние скорости потока через площадь поперечного сечения трубы i A
i= характерная площадь поперечного сечения трубы ζ
i= коэффициент потерь на трение для труб, фитингов и т. д. Q = расход k = коэффициент пропорциональности При указанных условиях теперь можно задать параболу характеристики системы:
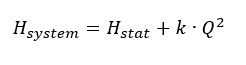
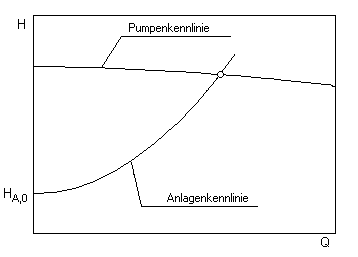
Коэффициент пропорциональности k определяется исходя из желаемой рабочей точки. Пересечение характеристики системы с кривой дроссельной заслонки конкретного насоса (характеристика насоса) представляет собой фактическую рабочую точку.
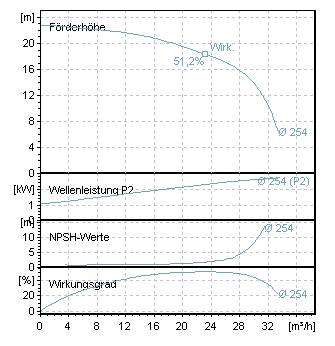
В дополнение к характеристической кривой Q-H, в центробежных насосах часто можно встретить следующие характеристические кривые: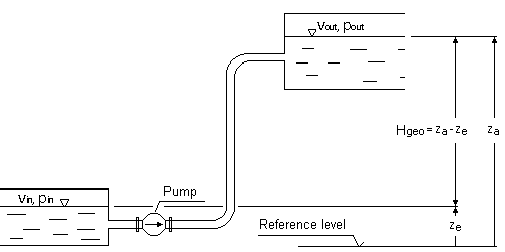
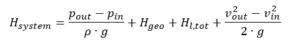pin, pout= давления при всасывании или выпуске уровня жидкости ρ = плотность жидкости g = ускорение свободного падения (9,81 м / с²) Hgeo= статическая разница высот между уровнем жидкости в емкостях на стороне всасывания и на стороне нагнетания. Hl, tot= общие потери на трение трубы между входом и выходом vin, vout= средние скорости потока во всасывающем и напорном контейнерах Согласно закону непрерывности, средние скорости потока во всасывающем и напорном резервуарах в большинстве случаев незначительно малы и ими можно пренебречь, если поверхности резервуаров относительно велики по сравнению с поверхностями трубопроводов. В этом случае приведенная выше формула упрощается до:
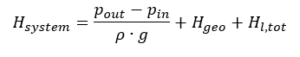Статическая часть характеристики системы, т.е. та часть, которая не зависит от скорости потока и, следовательно, расхода, равна:
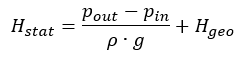Для закрытых систем это значение равно нулю. Общая сумма потерь складывается из потерь всех компонентов всасывающего и напорного трубопроводов. При достаточно больших числах Рейнольдса он пропорционален квадрату объемного расхода.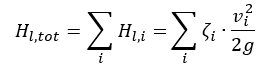
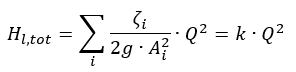g = ускорение свободного падения (9,81 м / с²) Hl, tot= общие потери на трение между входом и выходом vi= средние скорости потока через площадь поперечного сечения трубы i Ai= характерная площадь поперечного сечения трубы ζi= коэффициент потерь на трение для труб, фитингов и т. д. Q = расход k = коэффициент пропорциональности При указанных условиях теперь можно задать параболу характеристики системы:
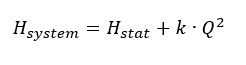Коэффициент пропорциональности k определяется исходя из желаемой рабочей точки. Пересечение характеристики системы с кривой дроссельной заслонки конкретного насоса (характеристика насоса) представляет собой фактическую рабочую точку.
