Niezbędną wysokość tłoczenia pompy w nierozgałęzionym rurociągu otrzymuje się z równania BERNOULLI dla jednowymiarowych, stacjonarnych przepływów mediów nieściśliwych:
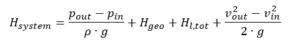
p
in, p
out= ciśnienia podczas zasysania lub odprowadzania poziomów cieczy ρ = gęstość cieczy g = przyspieszenie ziemskie (9,81 m / s²) H
geo= statyczna różnica wysokości między poziomem cieczy w zbiorniku po stronie ssawnej i tłocznej H
l, tot= całkowita strata tarcia w rurze między wlotem a wylotem v
in, v
out= średnie prędkości przepływu w zbiornikach po stronie ssącej i tłocznej Zgodnie z prawem ciągłości, średnie prędkości przepływu w zbiornikach po stronie ssącej i ciśnieniowej są przeważnie nieznacznie małe i mogą być pominięte, jeśli powierzchnie zbiorników są stosunkowo duże w porównaniu z powierzchniami rurociągów. W tym przypadku powyższy wzór jest uproszczony do:
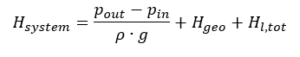
Część statyczna charakterystyki systemu, czyli część niezależna od prędkości przepływu, a tym samym od natężenia przepływu, to:
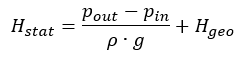
W przypadku systemów zamkniętych ta wartość wynosi zero. Całkowita wielkość strat składa się ze strat ze wszystkich elementów linii ssącej i ciśnieniowej. Przy wystarczająco dużych liczbach REYNOLDS jest proporcjonalna do kwadratu strumienia objętości.
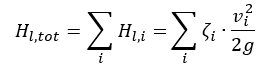
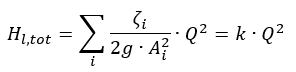
g = przyspieszenie ziemskie (9,81 m / s²) H
l, tot= całkowita utrata tarcia między wejściem a wyjściem v
i= średnie prędkości przepływu przez pole przekroju rury i A
i= charakterystyczna powierzchnia przekroju rury ζ
i= współczynnik strat tarcia dla rur, kształtek itp. Q = natężenie przepływu k = współczynnik proporcjonalności W podanych warunkach można teraz określić parabolę charakterystyki systemu:
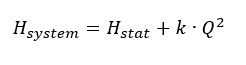
Współczynnik proporcjonalności k jest określany na podstawie pożądanego punktu pracy. Przecięcie charakterystyki systemu z krzywą dławienia specyficzną dla pompy (charakterystyka pompy) przedstawia rzeczywisty punkt pracy.
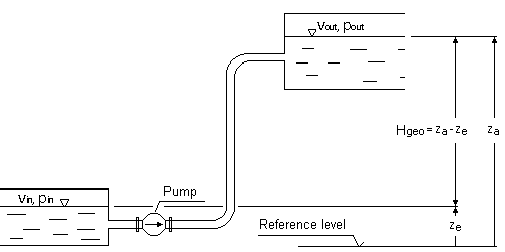
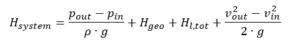pin, pout= ciśnienia podczas zasysania lub odprowadzania poziomów cieczy ρ = gęstość cieczy g = przyspieszenie ziemskie (9,81 m / s²) Hgeo= statyczna różnica wysokości między poziomem cieczy w zbiorniku po stronie ssawnej i tłocznej Hl, tot= całkowita strata tarcia w rurze między wlotem a wylotem vin, vout= średnie prędkości przepływu w zbiornikach po stronie ssącej i tłocznej Zgodnie z prawem ciągłości, średnie prędkości przepływu w zbiornikach po stronie ssącej i ciśnieniowej są przeważnie nieznacznie małe i mogą być pominięte, jeśli powierzchnie zbiorników są stosunkowo duże w porównaniu z powierzchniami rurociągów. W tym przypadku powyższy wzór jest uproszczony do:
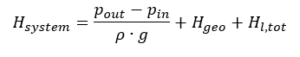Część statyczna charakterystyki systemu, czyli część niezależna od prędkości przepływu, a tym samym od natężenia przepływu, to:
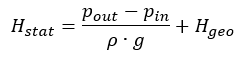W przypadku systemów zamkniętych ta wartość wynosi zero. Całkowita wielkość strat składa się ze strat ze wszystkich elementów linii ssącej i ciśnieniowej. Przy wystarczająco dużych liczbach REYNOLDS jest proporcjonalna do kwadratu strumienia objętości.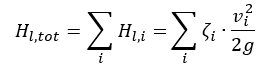
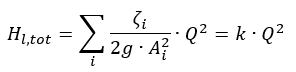g = przyspieszenie ziemskie (9,81 m / s²) Hl, tot= całkowita utrata tarcia między wejściem a wyjściem vi= średnie prędkości przepływu przez pole przekroju rury i Ai= charakterystyczna powierzchnia przekroju rury ζi= współczynnik strat tarcia dla rur, kształtek itp. Q = natężenie przepływu k = współczynnik proporcjonalności W podanych warunkach można teraz określić parabolę charakterystyki systemu:
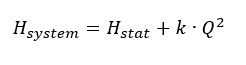Współczynnik proporcjonalności k jest określany na podstawie pożądanego punktu pracy. Przecięcie charakterystyki systemu z krzywą dławienia specyficzną dla pompy (charakterystyka pompy) przedstawia rzeczywisty punkt pracy.
