Potřebná dopravní výška čerpadla v nerozvětveném potrubí se získá z BERNOULLIHO rovnice pro jednorozměrné, stacionární proudění nestlačitelného média:
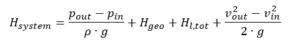
p
in, p
out= tlaky při nasávání nebo vypouštění hladin kapaliny ρ = hustota kapaliny g = tíhové zrychlení (9,81 m/s²) H
geo= statický výškový rozdíl mezi hladinou kapaliny v nádobách na sací a výtlačné straně H
l, tot= celková ztráta potrubí třením mezi vstupem a výstupem v
in, v
out= střední průtokové rychlosti v sacích a výtlačných nádobách Podle zákona kontinuity jsou střední rychlosti proudění v sacích a výtlačných nádržích většinou nevýznamně malé a lze je zanedbat, pokud jsou povrchy nádrží relativně velké ve srovnání s povrchy potrubí. V tomto případě je výše uvedený vzorec zjednodušený na:
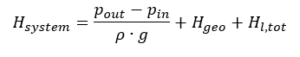
Statická část charakteristiky systému, tedy ta část, která nezávisí na rychlosti proudění a tedy na průtoku, je:
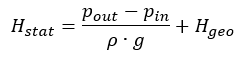
U uzavřených systémů je tato hodnota nulová. Celková ztrátová částka je tvořena ztrátami všech součástí sacího a tlakového potrubí. S dostatečně velkými REYNOLDSOVÝMI čísly je úměrná druhé mocnině objemového průtoku.
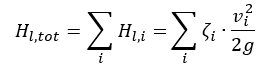
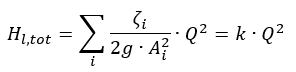
g = tíhové zrychlení (9,81 m/s²) H
l, tot= celková ztráta třením mezi vstupem a výstupem v
i= střední rychlosti proudění přes plochu průřezu potrubí i A
i= charakteristická plocha průřezu potrubí ζ
i= koeficient ztráty třením pro trubky, tvarovky atd. Q = průtok k = faktor proporcionality Za uvedených podmínek lze nyní specifikovat parabolu charakteristiky systému:
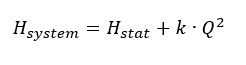
Faktor úměrnosti k se určí z požadovaného pracovního bodu. Průsečík charakteristiky systému s křivkou škrticí klapky specifickou pro čerpadlo (charakteristika čerpadla) představuje skutečný provozní bod.
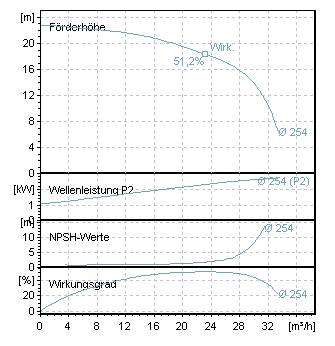
Kroměcharakteristiky Q-H lze u odstředivychčerpadel často nalézt následující charakteristiky:
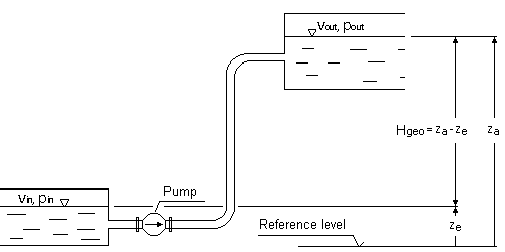
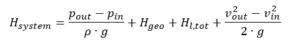pin, pout= tlaky při nasávání nebo vypouštění hladin kapaliny ρ = hustota kapaliny g = tíhové zrychlení (9,81 m/s²) Hgeo= statický výškový rozdíl mezi hladinou kapaliny v nádobách na sací a výtlačné straně Hl, tot= celková ztráta potrubí třením mezi vstupem a výstupem vin, vout= střední průtokové rychlosti v sacích a výtlačných nádobách Podle zákona kontinuity jsou střední rychlosti proudění v sacích a výtlačných nádržích většinou nevýznamně malé a lze je zanedbat, pokud jsou povrchy nádrží relativně velké ve srovnání s povrchy potrubí. V tomto případě je výše uvedený vzorec zjednodušený na:
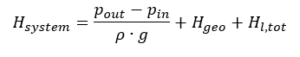Statická část charakteristiky systému, tedy ta část, která nezávisí na rychlosti proudění a tedy na průtoku, je:
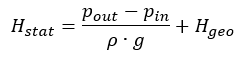U uzavřených systémů je tato hodnota nulová. Celková ztrátová částka je tvořena ztrátami všech součástí sacího a tlakového potrubí. S dostatečně velkými REYNOLDSOVÝMI čísly je úměrná druhé mocnině objemového průtoku.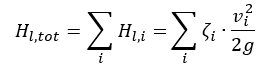
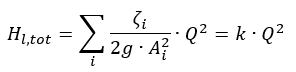g = tíhové zrychlení (9,81 m/s²) Hl, tot= celková ztráta třením mezi vstupem a výstupem vi= střední rychlosti proudění přes plochu průřezu potrubí i Ai= charakteristická plocha průřezu potrubí ζi= koeficient ztráty třením pro trubky, tvarovky atd. Q = průtok k = faktor proporcionality Za uvedených podmínek lze nyní specifikovat parabolu charakteristiky systému:
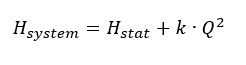Faktor úměrnosti k se určí z požadovaného pracovního bodu. Průsečík charakteristiky systému s křivkou škrticí klapky specifickou pro čerpadlo (charakteristika čerpadla) představuje skutečný provozní bod.
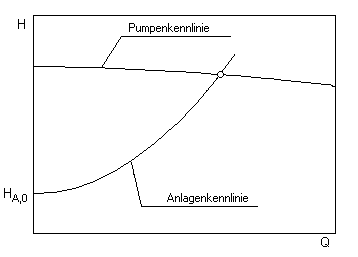
V uzavřených systémech (např. topné nebo chladicí okruhy) je geodetická výška nulová.
